Identity theorem for Riemann surfaces

In mathematics, the identity theorem for Riemann surfaces is a theorem that states that a holomorphic function is completely determined by its values on any subset of its domain that has a limit point.

Statement of the theorem

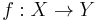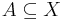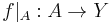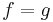Let $X$ and $Y$ be Riemann surfaces, let X be connected, and let $f�: X \to Y$ be holomorphic. Suppose that $f|_{A} = g|_{A}$ for some subset $A \subseteq X$ that has a limit point, where $f|_{A}�: A \to Y$ denotes the restriction of $f$ to $A$ . Then $f = g$ (on the whole of $X$ ).

References

Forster, Otto (1981), Lectures on Riemann surfaces, Graduate Text in Mathematics, 81, New-York: Springer Verlag, p. 6, ISBN 0-387-90617-7